一次完美的逃亡
- 3
- 2024-12-22 01:14:26
- 11

12部惊险刺激的丛林逃杀电影?
《丛林 》 (2017)
亚马逊丛林占据了世界雨林面积的一半,被人们称之为“地球之肺”,可见此秘境是天然的巨大氧吧,是各类动物们的天堂同时也是探险家们狂热追求的完美探险之地;影片中的主角贝纳在神秘导游的带领下与两位伙伴深入亚马逊丛林寻找那失落的黄金,当踏入丛林的那一刻,人类的文明世界就已远离。
《古墓丽影:源起之战 》
《勇敢者游戏:决战丛林 》
《一次完美逃亡》
编剧克里夫·安德森和希德妮这对看似新婚燕尔的小夫妻正驱车前往风景迷人的夏威夷度假,他们在当地结识了另一对情侣——极具野性的尼克和吉娜。在尼克夫妇的指引下,他们走入原始丛林探险,寻找从未有人涉足的完美之地。但是在此过程中,他们从其他游客那里听说了一对新婚夫妇狂乱杀人的恐怖传闻。美丽的小岛瞬间杀气腾腾,阴云密布,是去是留成为了一个艰难的选择。
lol小鱼人男刀秒人连招技巧?
首先估计血量,是否能击杀,然后R到人后:
1、E上去,引燃,落地时开wAAA,然后q到身后A一下,追着继续aa2、开wq上去,引燃,aaa看见要跑e上去,追着继续aa上面两种连招都是6级后的,6级前可以开着w,q上去a一下e回来如果对线小鱼人,我建议先q在e,也就是用2比较好,而且要等他用了e在放大,不然可以躲掉你的大。
就算你不放大,你和小鱼人拼时最好不要太激进,等他用了e在和他拼,不然你q过去e起来时他也e起来,等你掉下去他也掉下来压你,在wq反打一套,交个引燃你可能就死了。如何应对远程poke流的英雄?
如光辉这种他向你放技能,距离近就e到他旁边打一套,远的话靠自己走位躲来节约蓝如何应对突进流的英雄?
如阿卡丽面对突进和高爆发就塔下猥琐吧,多带些红蓝要消耗,等打野来就一套秒掉我玩小鱼人最怕的就是大发明家和阿卡丽了,各种消耗爆发,冲不是,不冲又被消耗死,只能等打野。。。
克里斯海姆斯沃特电影?
克里斯·海姆斯沃斯电影:
星际迷航、一次完美的逃亡、现金、雷神、林中小屋、复仇者联盟、白雪公主与猎人、赤色黎明、星际迷航:暗黑无界、雷神2:黑暗世界、极速风流、骇客交锋、海洋深处、复仇者联盟2:奥创纪元、假期历险记、猎神:冬日之战、超能敢死队、雷神3:诸神黄昏、12勇士、复仇者联盟3:无限战争、皇家酒店谋杀案、复仇者联盟4:终局之战、黑衣人:全球追缉、极限营救。
完美的他陆啸第几集逃脱?
第一次:陆啸逃出去看母亲,遇到可乐,为了避开追捕的人亲了可乐。
第二次:第十五集,陆啸逃出去的时候又遇到了可乐,可乐怕他被发现带他从密道回去了。
第三次:第十六集,可乐带路啸从密道逃脱。因为不是探视时间,陆啸没有见到母亲。
第四次:第十七集,陆啸装病,可乐偷偷带陆啸从密道逃出,陆啸见到了母亲。
后面还没有更新。
三次数学危机当初都解决了吗?
目前我们所学的数学体系相对比较完备,说明三次数学危机都基本解决。为了使读者更清晰的了解这个问题,下面谈一谈三次数学危机都是什么?并如何解决的?
第一次数学危机
早在古希腊时期,数学家毕达格拉斯认为,宇宙的一切都是数,而且是整数。当然,这里很多小朋友会误会,毕达哥拉斯所说的数,包括整数和整数的比,用我们今天的话来翻译,宇宙的一切都是由有理数组成。


后来他的学生希帕索斯,提出问题,边长为一的正方形的对角线如何用两个整数的比表示出来?这冲击了当时的希腊数学整个体系,你当时的数学家深感不安,这就是第一次数学危机。
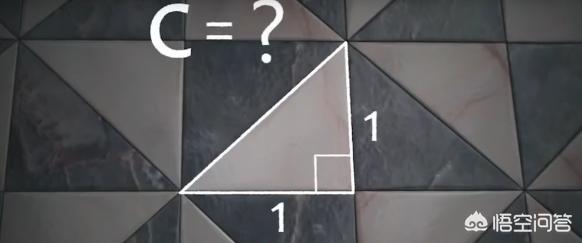
有一个说法,希帕索斯不仅提出这个问题,同时也给出过证明,彻彻底底推翻了比达格拉斯的理论,所以希帕索斯才惨遭毒手。至于是不是这样的就不得而知了。
第一次数学危机的解决表明,几何量不能完全用整数表示,反之,任何数却可以有几何量表示出来。直到人们认识了无理数,认识了实数系,第一次数学危机,算是彻底解决。也是这一次危机促成了公理几何与逻辑的诞生。
第二次数学危机
第二次数学危机于牛顿时代,此时已经诞生了微积分,就是牛顿-莱布尼茨站在巨人的肩膀上,开创了基于微积分的数学新时代!

这次危机的关键问题是无穷小量究竟是不是零?两种答案都会产生矛盾,如果无穷小量是零,那么凭什么他当分母?如果无穷小量不是零,那么,凭什么在计算中忽略它的存在。
第二次数学危机的解决,是著名数学家柯西引入了极限的概念,认为无穷小量和无穷大量都是变量,只不过无穷小量的极限是零而已。

第三次数学危机
所有的高中课本的第一节都是集合,而高中教材都会用一页纸的地方介绍集合论的创立人康托尔,康托尔的集合论也成为现代数学的基石,著名数学家庞加莱曾说过:借助集合论,我们可以建造整个数学大厦。这是对集合论最高的赞美。
众所周知,集合有三要素:“确定性,无序性,互异性”,这么简洁美丽的体系即将迎来前所未有的挑战!
几十年后,罗素悖论产生,提出者当然是罗素。他指出:如果一个理发师只给不自己理发的人理发。那么他应该给自己理发吗?细心的人发现,这个理发师怎么做都不对,并且又符合集合的定义,这个悖论严重挑战了集合中的“确定性”!
用集合的语言来说:如果存在一个集合A={x | x∉x },那么A∈A是否成立?如果它成立,那么A∈A,不满足A的特征性质。如果它不成立,A就满足了特征性质。
后来,德国数学家策梅罗,寻找到一种解决办法,把集合论建立在一组公理之上,目的是回避悖论。后来通过一系列数学家的完善,形成了一个集合论的公理系统,在这个系统之内没有悖论。这套系统也叫做“ZF公理系统”

当然,也有这样的说法,认为第三次数学危机表面上解决了,其实不是解决了,是回避了悖论,然而,数学的确定性却逐渐消失,实质上,第三次数学危机以更深刻的形式在延续着,至今没有解决。
你有什么样的看法呢?欢迎来讨论。

到此,以上就是小编对于一次完美的逃亡的问题就介绍到这了,希望介绍关于一次完美的逃亡的5点解答对大家有用。